FUNCIÓN CUADRÁTICA
https://thales.cica.es/rd/Recursos/rd99/ed99-0416-02/caratula.gif
La forma general de una función cuadrática es f ( x ) = ax 2 + bx + c . La gráfica de una función cuadrática es una parábola , un tipo de curva de 2 dimensiones.
La función del coeficiente a en la ecuación general es de hacer la parábola "más amplia" o "más delgada"
Si el coeficiente de x 2 es positivo, la parábola abre hacia arriba; de otra forma abre hacia abajo.
http://www.monografias.com/trabajos60/funcion-cuadratica-simulador/Image3.gif
El vértice de una parábola es el punto en la parte baja de la forma "U" (o la superior, si la parábola abre hacia abajo).
La ecuación para una parábola también puede escribirse en la "forma vértice":
y = a ( x – h ) 2 + k
En esta ecuación, el vértice de la parábola es el punto ( h , k ).
El coeficiente de x aquí es – 2 ah . Esto significa que en la forma estándar, y = ax 2 + bx + c , la expresión -b/2a
nos da la coordenada en x del vértice .
http://www.matematicasvisuales.com/images/analysis/derivative/quadratic/cuadratic13Sp.jpg
El eje de simetría
El eje de simetría de una parábola es la recta vertical a través del vértice. Para una parábola en la forma estándar, y = ax 2 + bx + c , el eje de simetría tiene la ecuación
x= -b/2a
Dese cuenta que – b /2 a es también la coordenada en x del vértice de la parábola.
http://www.iesarroyodelamiel.es/matematicas/materiales/4eso/funciones/teoriafuncioncuadratica/teoria52.gif
Intercepciones
Puede encontrar la intercepción en y de una parábola simplemente al introducir 0 para x . Si la ecuación esta en la forma estándar, entonces Usted solo toma a c como la intercepción en y . Por ejemplo, en el ejemplo anterior:
y = 2(0) 2 + (0) – 1 = –1
Así la intercepción en y es – 1.
Las intercepciones en x son un poco más complicadas. Puede usar la factorización , o completar el cuadrado , o la fórmula cuadrática para encontrar estas (si es que existen!).
https://image.slidesharecdn.com/actividadno2moduloiv-131102105719-phpapp01/95/grfica-de-una-funcin-cuadrtica-14-638.jpg?cb=1383390852
en este caso resolveremos 2 ejercicios de función cuadrática en 4 pasos:
1º paso: encontrar el sentido de la curva
2º paso: hallar el eje de simetría
3º paso: hallar el vértice
4º paso: hallar interceptos con x y y
ejercicio Nº 5
su gráfica:
ejercicio Nº17
su grafica:
2. un proyectil es disparado verticalmente hacia arriba desde una altura de 600m sobre el suelo. su altura h(t) en metros sobre el suelo, despues de t segundos, esta dada por:
a.¿cual es la altura del proyectil despues de 1 seg?
b. ¿despues de cuanto tiempo vuelve a estar en una altura de 600m sobre el suelo?
c.¿cual es la altura maxima que alcanza? ¿cuanto tiempo gasta para alcanzarla?
GRAFICA
https://www.youtube.com/watch?v=7mLBvcaKLg0&t=88s

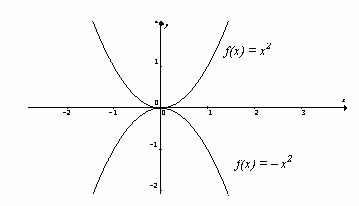












Excelente trabajo me gusto mucho el blog,y tiene buena información con la que se pueden despejar dudas.
ResponderEliminarmuy buena informacion, esta todo muy completo... el video tambien me ayudo mucho a comprender lo que con la teoria no podia. gracias
ResponderEliminarQue buena manera de explicar los ejercicios, ya que muchas personas no entienden solamente con las imágenes así que pienso que los vídeos fue un muy buen recurso.
ResponderEliminarmuchas gracias, me agrado mucho el blog. ahora si puedo hacer con facilidad mi blog. gracias :)
ResponderEliminar